Atik Infinity Colour Camera - Field of View (FOV)

Introduction | Field of View of the Atik Infinity Camera | Empirical Comparison with Astronomy.tools Field of View Calculator | Unknown Extension/Reduction Factor | Conclusions | Links

Archive

On this page, I present some information about the field of view of my Atik Infinity Colour* camera. Possibly, these are useful for others who want to acquire this camera as well...

See also pages (Archive):

*) Usually, I would write "Color", because I try to use American English, but Atik is a company located in the UK, and therefore it's "Colour"...

Note: Over Christmas 2022, I sold my Atik Infinity camera (transferred on January 5, 2023). I therefore cannot report any further experiences with it here.

 

Introduction

Of course, one might wonder how large the field of view (FOV) of the Atik Infinity camera is when you connect it to a particular telescope, because this determines whether you will see sky objects completely or only partially, small or large. Some nebulae and open star clusters, as well as the Andromeda galaxy M 31, are widely extended, often over several degrees, whereas others, such as globular star clusters or the Ring Nebula M 57, are just a few arcminutes wide. If you know the field of view that you get with the Atik Infinity at a certain telescope and, if necessary, with focal length extenders or reducers, then you know what you can expect and which objects can be sensibly approached for observation.

This page is therefore dedicated to the topic of "field of view" (FOV), starting with formulae that contain the focal length of the telescope as a key element (including reducers for the Celestron C8 and C5). I also show how I compared my results empirically with the results of an online calculator for determining the field of view and that I found a sufficient match.

But what can you do if, for example, you cannot trust the listed reduction factor of 2 or 3, especially if the manufacturer already indicates that the factor depends on the specific conditions? At the end of this page, I therefore present one or more approaches to determine the field of view and the (here: reduction) factor under these conditions.

 

Field of View of the Atik Infinity Camera

Of course, one might ask how large the field of view of the camera is when you connect the Atik Infinity to a specific telescope. In the following you will find some formulae for calculating this and a table with results for some selected telescopes (mostly mine...).

Angular Resolution - Formulae

Atik provides a formula that specifies the angular resolution (in seconds) of the Atik Infinity camera per pixel:

As you can see, only the focal length of the telescope is of interest. In order to obtain the field of view for the sensor of the camera, one has to multiply this value by the number of pixels of the corresponding sensor side (see also the formula of Oden below).

Peter Oden provides an alternative formula (but with the same origin...) for the angle (given in degrees) and the width or height of the sensor (in mm):

Thus, we get the following rules of thumb for the FOV:

Using the values of the Sony sensor (6.45 μm, 1392 pixels horizontally), this results in a width of 9 mm for this sensor. Used in Oden's formula, one gets, unsurprisingly, the same values as for the Atik formula...

The factor of "206.3" in the Atik formula appears like "fallen from the sky", but can be elucidated with the help of Oden's formula; it could be composed of like this:

3.6 * (180 degrees / pi) = 3600/1000 * (180 degrees / pi) = 206.26

The factor "3600" might result from the Atik formula indicating the angle in seconds. The dividend "1000" is probably due to the conversion from mm to μm.

Table

The following table lists the field of view for my current, some older, and some "typical" telescopes obtained by the formulae above:

   
Angular Resolution of the Atik Infinity Camera
Telescope Examples
Focal Length (mm)
1 Pixel (Sec)*
Sensor (Sec)
Sensor (Min)
Sensor (Deg)
 FOV**
PS 72/432
432
3.08
4287.60
71.46
1.19
 1.19° x 0.89°
Heritage 100P
400
3.33
4630.61
77.18
1.29
  
4,5" Newton
450
2.96
4116.10
68.60
1.14
  
4,5" Newton, Heritage 114N
500
2.66
3704.49
61.74
1.03
  
5" Newton, Heritage P130
650
2.05
2849.61
47.49
0.79
  
TLAPO1027
714
1.86
2594.18
43.24
0.72
 0.72° x 0.54°
6" Newton, Explorer 150PDS
750
1.77
2469.66
41.16
0.69
  
6" Newton
900
1.48
2058.05
34.30
0.57
  
6"/8" Newton, GSD 680
1200
1.11
1543.54
25.73
0.43
  
Skymax-102
1300
1.02
1424.80
23.75
0.40
  
Skymax-127
1500
0.89
1234.83
20.58
0.34
 0.34° x 0.26°
Celestron C8
2032
0.65
911.54
15.19
0.25
 0.25° x 0.19°
Celestron C8R (f/6.3 R/C)
1280
1.04
1447.07
24.12
0.40
 0.40° x 0.30°
Celestron C5
1250
1.06
1481.80
24.70
0.41
 0.41° x 0.31°
Celestron C5R (f/6.3 R/C)
787.5
1.69
2352.06
39.20
0.65
 0.65° x 0.49°
eVscope
450
1.72
0.61
 0.61° x 0.46°
Vespera
200
2.99
    
1.6
 1.6° x 0.9°

italic: Not (or no longer) owned by me; *) also called "image scale" (ideally beween 1 and 2); **) calculated with astronomy.tools

Graphic

Figure: FOV for my current telescopes at the Atik Infinity camera (created with Astronomy.tools)

 

Empirical Comparison with Astronomy.tools Field of View Calculator

Heritage 100P

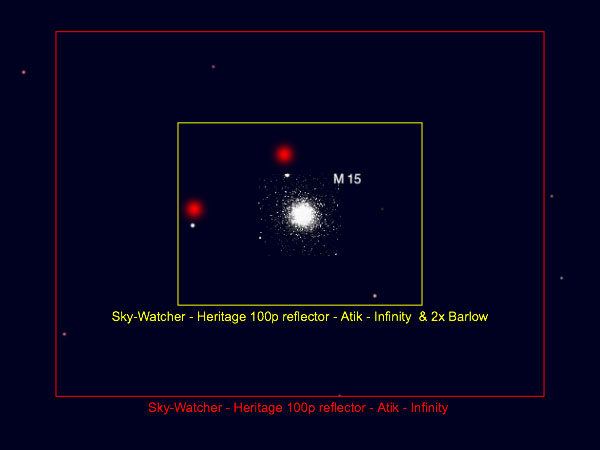
In the following, I describe an empirical test in which I measured the field of view in two photos with the help of two prominent stars and compared this data with the results of an online field of view calculator using the same stars.

First, I calculated the field of view using the field of view calculator on Astronomy.tools (Website provided by First Light Optics Ltd). I entered the Heritage 100P, the Atik Infinity camera, and once a 2 x Barlow lens and once again "without Barlow lens." I compiled both results in one picture (this is easily done with the online calculator) that is presented below at the center. For the following, the field of view frames and the two "measurement stars" are needed.

In addition, I used two post-processed and turned upside-down versions of original images of M 15. I scaled them down from 1392 pixels to the size of the corresponding field of view frames frames in the simulation (one 490 pixels wide, one 245 pixels wide). And this is how my results looks like:

   

M 15 with Heritage 100P (FL = 400 mm, fuzzy), processed

 

Simulation for M 15 with Heritage 100P, with (yellow) and without (red) 2 x focal extender

  

M 15 with Heritage 100P and 2 x focal extender (FL = 800 mm), processed

Star distance: 108 H, 12 V => 108.7

 

Star distance: 96 H, 50 V = 108.2

 

Star distance: 109 H, 8 V = 109.3

FOV: 1.28° x 0.96° (1.29° own calculation)

      

FOV: 0.64° x 0.48° (0.64° own calculation)

For comparing the fields of view, I measured the distance between two prominent stars, horizontally and vertically, using a marquee rectangle in Photoshop Elements. I determined the length of the diagonal, that is the distance, according to the theorem of Pythagoras*; die results are given below the images. In both of my pictures, the distance is slightly larger than in the simulation, but I think that the match is sufficient.

I regard the prediction of the field of view simulator as useful, even though the photos of the object, here M 15 in Pegasus, that are shown in the simulation, will certainly not have much in common with what you actually see and photograph...

*) Actually, spherical trigonometry would have to be used, but for small angles, the "planar" geometry is a good enough approximation (and easier to calculate).

In the meantime, I was pointed to another field of view calculator on the Sky at Night Magazine (BBC) Website!

 

Unknown Extension/Reduction Factor

Skymax-127

I have only photographed the Pleiades M 45 and the Andromeda Galaxy M 31 with the Skymax-127 so far. Because these are extended objects, I used my 2 x TS focal reducer with an 25mm extension tube. For this combination, the manufacturer lists a reduction factor of 3 x, but notes that this factor depends on the actual conditions.

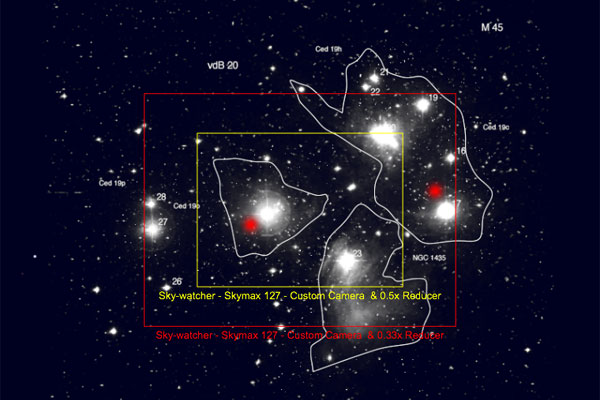
I tried to empirically determine the actual reduction factor using Astronomy.tools and a photo that I took of M 45 (Pleiades), using the pixel distance between Alcyone and Electra as a "scale." For this, I let the fov tool draw frames for a 2 x and a 3 x focal reducer and set the star distance in relation to the total widths of the frames. I did the same for the photo.

These are the photo and the simulation image that I used:

    

M 45 taken with Skymax-127 and focal reducer, the distance between Alcyone and Electra was used as "measure"

 

Simulation for M 45 with Skymax-127 and 2 x (yellow) and 3 x focal reducer (red)

Using the reverse rule of three, I was finally able to determine the reduction factor via the frames for the 2 x and the 3 x reducer, the latter value being more accurate because of the larger pixel numbers. The following table provides an overview of the calculations:

  Original Photo 3 x Focal Reducer 2 x Focal Reducer
Picture/Frame Size 1392 x 1040 396 x 296 260 x 196
Star Distance, Relation to Image Width Alcyone - Electra = 1055 pix* = 0.7579 of the width Alcyone - Electra = 228 pix = 0.5758 of the width Alcyone - Electra = 228 pix = 0.8769 of the width
Calculating the Reduction Factors Using the Reverse Rule of Three x = 2.25 (see below**) 3*0.5758 = x*0.7579
x = 3*0.,5758/0.7579=2.23		 2*0.8769=x*0.7579
x = 2*0.8769/0.7579=2.31

*) Measured rotated so that the connecting line was horizontal. **) Since the 3 x reducer has larger numbers in the calculation, I chose a value for the factor that is closer to this value...

I calculated a factor of about 2.25 (instead of 3) for this combination. This leads to the following values for the Skymax-127:

All values are, of course, only approximate because of the inaccuracies involved!

Skymax-127 - Alternative Approach

Because the approach using the field of view calculator is somewhat inaccurate, I also tried a second approach, but this one is more complex and based on determining the angular distance between two prominent stars in the photo. I did the following:

    

Online calculator für den distance between stars (Harald Greier)

 

Excel spreadsheet for the calculation of the distance between stars (Schulbiologiezentrum Hannover)

Figure: Both calculators that I used arrived at the same result...

Both calculators arrived at a star distance of 0.6 degrees (or 35' 43"). I had measured a pixel distance of 1055 pixels between the stars in the photo. This is 0.7579 of the width in relation to the sensor width of 1392 pixels. On the other hand, the photo is 1.32 times wider than the stellar distance, leading to a field of view of 0.79 ° or 2850" = 47.5' = 47' 30", which is a little more than what I had calculated using the other method.

Now only the reduction factor and effective focal length and aperture are missing! For the telescope, my Excel spreadsheet lists a field of view of 20.58'. When I divide the above-mentioned field of view of 47.5' by this value, I get 2.31 (exactly: 2.308), that is, the value that I had already determined using the 2 x reducer frame. So I was wrong, as far as the accuracy of the above estimates is concerned! This leads to the following values for the Skymax-127 with 2 x d focal reducer and 25 mm extension tube:

All values are, of course and despite of the many calculations, only approximate because of the inaccuracies involved! And as I demonstrated, there is also a way without the help of the field of view calculators from Astronomy.tools or the Sky at Night Magazine.

 

Conclusions

On this page, I laid down the fundament for determining the field of view of the Atik Infinity camera at different telescopes and with focal length extenders and reducers, even in the case that the extension or reduction factors are not exactly known. Other hobby astronomers should be able to transfer this to their equipment.

Note: Over Christmas 2022, I sold my Atik Infinity camera (transferred on January 5, 2023). I therefore cannot report any further experiences with it here.

 

Links

 

An den Anfang   Homepage  
gerd (at) waloszek (dot) de

About me
made by walodesign on a mac!
07.10.2024