About Focal Length, Aperture, and Depth of Field for Different Sensor Sizes

Introduction | Sensor Size and Crop Factor | Question 1: Angle of View, Focal Length, and Sensor Size | Question 2: Depth of Field, Aperture, and Sensor Size | Question 3: Should I Replace My Compact Camera with a System Camera or DSLR to Attain a Larger Depth of Field? | Question 4: Using Depth of Field Markers | Summary | References

On this page, I want to touch the topic "focal length, aperture, and depth of field (DOF) for different sensor sizes." Specifically, I will discuss the questions:

  1. Which focal lengths produce the same angle of view on cameras using different sensor sizes? How can I calculate this?
  2. What does a nominally identical aperture value mean for cameras using different sensor sizes as to light intensity an depth of field?
  3. Should I replace my compact camera with a system camera or DSLR to attain a larger depth of field?
  4. What do the DOF markers on a lens mean for you if you use the lens with a camera that has a sensor of a different size than that for which the lens was designed.

 

Introduction

As users of digital cameras, we know that cameras using a small sensor have a much greater depth of field than those with a larger sensor - and as one is used from film cameras. This is apparent in many shooting situations, but particularly when shooting macros. The larger depth of field makes the shooting, at least the focusing, much easier especially for beginners, but also for street photographers, as an example. On the other hand, photos with large depth of field - ideally, going from front to back - often look boring. Therefore, advanced amateur and professional photographers like to discuss just the opposite: how to get the lowest possible depth of field to separate the photographed object from the background? This is often associated with a "bokeh" discussion (how "pleasantly" the blurred region are shown). Often, these photographers are not satisfied with the depth of field that can be achieved with APS-C cameras. For them, only so-called full-frame cameras (corresponding to the 35 mm film format) are sufficient. At best, one can achieve a shallow depth of field using APS-C, MFT or 1" sensor cameras, when approaching the object to be photographed closely and opening aperture as wide as possible (if the lens will allow this...).

Since cell phone cameras make life difficult for simple and cheap digital cameras, many camera manufacturers have started, to launch "advanced" compact cameras on the market, which, while still having compact dimensions, are distinguished by especially two features: (1) larger sensor and (2) bright optics (frequently only at the wide end). Prospects for such cameras, but, of course, other photographers as well therefore face questions such as:

As announced above, I will address these and other questions below.

 

Sensor Size and Crop Factor

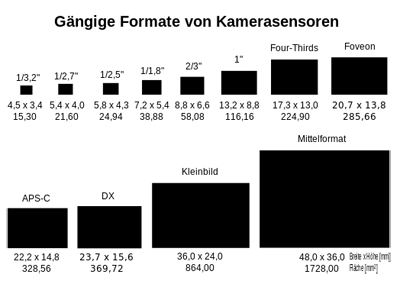
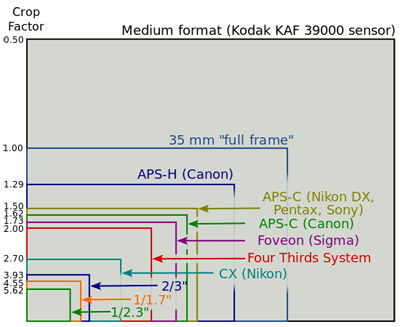
I will start with a few comments on sensors of different sizes. For historical reasons, different types of names are used, which often tell little about the actual sensor size. Most important for the following is a number that is called the "crop factor." It indicates the ratio between the diagonal of the full-format sensor and the diagonal of a sensor of a certain format (or the ratio of the respective angles of view, see below). This number will always accompany us in the discussion below. The following table lists dimensions and crop factors for important sensor types:

Format Full-frame Format APS-C (DX) APS-C (Canon) Foveon (Sigma) MFT MFT multi-aspect 1" 2/3" 1/1.7" 1/1.8" 1/2.3"
Dimensions (mm) 36 x 24 23.7 x 15.6 22.3 x 14.9 20.7 x 13.8 17.3 x 13.0 variable 13.2 x 8.8
12.8 x 9.3 		8.8 x 6.6 7.6 x 5.7 7.2 x 5.4 6.2 x 4.62
Area (mm2) 864 370 329 286 225 variable 116
119		 58 43 39 29
Diagonal (mm) 43.3 28.4 27.1 24.9 21.3 20? 16 11 9.5 8.9 7.7
Crop Factor 1.0 1.5 1.6 1.7 2.0 2.2 2.7 4 4.6 4.9 5.6

The values for the dimensions of the various sensor types differ slightly in the various sources. Here, I essentially follow Wikipedia Wikipedia (Formatfaktor). Many of the values are rounded.

Below are two diagrams from Wikipedia on this topic:

    

 

Question 1: Angle of View, Focal Length, and Sensor Size

The angle of view determines how much of a photographed scene is projected onto the sensor and thus appears on the photo (for the usual rectangular image format, this is usually the the value for the image diagonal). Lenses that create different viewing angles differ in their focal lengths and thus allow you to capture a "normal" viewing impression (normal lenses), large parts of the scene (wide angle lenses), or just a small section of it (telephoto lenses). Since the 35 mm film format dominated photography in the past, people usually do not speak of viewing angles, but of focal lengths instead (wide angle, normal, telephoto focal length) to describe the behavior of lenses.

To achieve the same visual impression with cameras using sensors of different sizes, lenses with different viewing angles / focal lengths have to be used. For a very small sensor, for example, a focal length that would result in a wide-angle lens at full frame format, already represents a telephoto lens. Therefore, people use to convert focal lengths of all digital cameras to "35 mm equivalent" values in order to compare them more easily. And not surprisingly, the crop factor comes into play here:

Camera Examples

The following table lists data of some cameras, particularly of those that my wife or I own(ed) or that I find interesting:

   
Focal Length
Crop
Factor
short (wide end)
long (tele end)
Camera Sensor Size actual 35 mm equiv. actual 35 mm equiv.
Any... Full-frame format 1   identical
with actual		   identical
with actual
Leica X Vario APS-C (DX) 1.5 18 mm 28 mm 46 mm 70 mm
Ricoh GR APS-C (DX) 1.5 18.3 mm 28 mm --- ---
Ricoh GXR A16 APS-C (DX) 1.5 15.7 mm 24 mm 55.5 mm 85 mm (83.5 mm)
Panasonic GM5 (Kit) MFT 2 12 mm 24 mm 32 mm 64 mm
Panasonic LX100
Leica Digilux 109 		MFT multi-aspect 2.2 10.9 mm 24 mm 34 mm 75 mm
Sony RX100 M1-2 1" 2.7 10.4 mm 28 mm 37.1 mm 100 mm
Sony RX100 M3-5 1" 2.7 8.8 mm 24 mm 25.7 mm 70 mm
Panasonic LX1000
Leica VLux 114 		1" 2.7 9.1 mm 25 mm 146 mm 400 mm
Panasonic TZ202 1" 2.7 8.8 mm 24 mm 132 mm 360 mm
Ricoh GX100/200
Ricoh GXR S10		 1/1.7" 4.6 5.1 mm 24 mm 15.3 mm 72 mm
Panasonic LF1 1/1.7" 4.6 6.0 mm 28 mm 42.8 mm 200 mm
Ricoh CX4
Ricoh GXR P10		 1/2.3" 5.6 4.9 mm 28 mm 52.5 mm 300 mm

The technical specifications of the cameras and, especially, the advertising of the camera manufacturers often list the 35 mm equivalent focal lengths instead of the actual ones, which can easily lead to misunderstandings. Sometimes, it is not easy to retrieve the actual focal lengths, but most of the time they are still written on the front of the lens ...

 

Question 2: Depth of Field, Aperture, and Sensor Size

Now I want to address my second question that I asked at the beginning, here in a somewhat generalized form: What does the same aperture value mean for a camera with a smaller sensor and for a full-frame camera? There are two answers to this:

This reads so complicated that I explained it incorrectly on this page in my first attempt. But after all, it is easy to understand: To attain the aperture value that determines the depth of field, simply multiply the aperture value that you set at the camera with the sensor's crop factor.

Here are some examples:

Since full aperture steps are graded with a factor of √2 (1.414 ...), one can state that the depth of field of an APS-C camera corresponds to about a full-frame camera that has been dimmed by a full f-stop compared with the APS-C camera. For the MFT format, this will already be two full stops.

In an article entitled Sensorgröße und Schärfentiefe (by Prophoto GmbH), the following advantages and disadvantages are mentioned:

Camera Examples

The following table adds aperture-related data for the cameras above:

 
Initial Aperture
Min. Aperture**
Focal Range
Camera Sensor Size Crop Factor nominal for DOF nominal for DOF nominal equivalent
Any... Full format 1 1.0... like
nominal 		16 - 32 like
nominal 		depends on lens like
nominal
Leica X Vario APS-C (DX) 1.5 3.5 - 6.4 5.6 - 9.6 16 24 18 - 46 mm 28 - 70 mm
Ricoh GR APS-C (DX) 1.5 2.8 4.2 16 24 18.3 mm 28 mm
Ricoh GXR A16 APS-C (DX) 1.5 3.5 - 5.5 5.6 - 8.25 16 24 15.7 - 55.5 mm 24 - 85 mm
Panasonic GM5 (Kit) MFT 2 3.5 - 5.6 7 - 11.2 22 44 12 - 32 mm 24 - 64 mm
Panasonic LX100
Leica Digilux 109 		MFT
multi-aspect		 2.2 1.7 - 2.8 3.74 - 6.16 16 35.2 10.9 - 34 mm 28 - 75 mm
Sony RX100 M1-2 1" 2.7 1.8 - 4.9 4.86 - 13.23 11 29.7 10.4 - 37.1 mm 28 - 100 mm
Sony RX100 M3-5 1" 2.7 1.8 - 2.8 4.86 - 7.56 11 29.7 8.8 - 25.7 mm 24 - 70 mm
Panasonic LX1000
Leica VLux		 1" 2.7 2.8 - 4 7.56 - 10.8 11 29.7 10.9 - 34 mm 25 - 400 mm
Panasonic TZ202 1" 2.7 3.3 - 6.4 8.91 - 17.28 8 21.6 8.8 - 132 mm 24 - 360 mm
Ricoh GX100/200
Ricoh GXR S10 		1/1.7" 4.6 (4.55) 2.5 - 4.4 11.38 - 20.0* 8? ? 5.1 - 15.3 mm 24 - 72 mm
Panasonic LF1 1/1.7" 4.6 (4.55) 2.0 - 5.9 9.1 - 26.85* 8 36.4 6.0 - 42.8 mm 28 - 200 mm
Ricoh CX4
Ricoh GXR P10		 1/2.3" 5.6 3.5 - 5.6 19.6 - 31.36 5.6? 31,36? 4.9 - 52.5 mm 28 - 300 mm

*) Calculated with crop factor 4.55; **) the minimum aperture leads to the maximum DOF but often is plagued with blur that is introduced by diffraction

At a specific focal length, the aperture range is limited by the initial and the maximum aperture. And this limits the differences in DOF that you can achieve with a camera.

The table above is not well suited to a more precise comparison of cameras with different sensors with regard to the depth of field behavior. It is better to select a certain aperture (f/5,6, f/8,...), which all cameras can set, and a certain "equivalent" focal length, so that all cameras have (approximately) the same viewing angle. It then shows that, ultimately, the depth of field depends on the "DOF-relevant" aperture only. To put it simply, the larger the aperture value, the larger the DOF is. I determined all this "empirically," although the answers to question 2 already say so. After having calculated several aperture values and two focal lengths, I got approximately the same depth of field for cameras with sensors of different sizes at different apertures (with the crop factor as ratio). However, due to certain inaccuracies in the input data, there were no exact matches, but the "principle" was clearly discernible. More on this when I discuss question 3!

 

Question 3: Should I Replace My Compact Camera with a System Camera or DSLR to Attain a Larger Depth of Field?

According to what was said in the introduction, this question sounds somewhat absurd, because there was claimed that compact cameras with a small sensor have a much greater depth of field than cameras with a large sensor. I admittedly accepted that statement without ever really checking it - until a friend asked me the following question in connection with close-up/macro photography:

Even with cameras with small sensors, the depth of field at close distances is often so small that the desire for more depth of field arises! But would cameras with a large sensor be an alternative?

When I was confronted with this question, I had already forgotten that I had created this page and that it basically contained the answer. So I went, as already indicated above, the empirical and somewhat laborious path using the exemplary calculations of the depth of field. The depth of field formulae seemed too complex to me for a quick answer, and so I looked for a suitable depth of field calculator, which I found at Vision Doctor. Among other things, it needed the circle of confusion and the actual focal length (not the equivalent!) as input data. Since it was only a matter of principle, I chose an equivalent focal length of 28 mm to get the same section/angle of view for the different cameras, and converted them for the respective sensors to the actual focal length using the corresponding crop factor (if this was not already in the technical data). I also chose an aperture of f/8 and a distance of 50 cm. In addition, the effective aperture for the depth of field was calculated according to the above formula. The data clearly showed that the depth of field decreased with increasing sensor size for the same aperture value. Since this did not quite satisfy me yet, I created a larger table with more f-stops. In this table, I was quickly able to see that the "DOF-relevant" aperture always produced approximately the same depth of field. Thus, I had empirically found what I could have already known without all this work... Well, that was written as a "statement" without justification in an article,and now I found it out with my own eyes... Actually, the formula for the depth of field could have provided and justified this result - but this approach seemed way too complicated to me...

Here is an excerpt from my calculations to illustrate my writing:

Equivalent Focal Length: 28 mm, Distance: 50 cm Set
Focal Length
Set Aperture: f/8
Set Aperture: f/5.6
Camera/Camera Type Sensor Type Crop Factor DOF DOF-relevant Aperture DOF DOF-relevant Aperture
Ricoh CX4 1/2.3" 5.6 5.0 (4.9) mm 2142.65 mm? 44,8? 821.67 mm 31.4
Pana LF1 1/1.7" 4.6 (4.55) 6.0 (6.1) mm 1176.36 mm 36,8 601.42 mm 25.8
Sony RX100, Pana TZ202 1" 2.7 10.4 mm 481.67 mm 21,6 311.54 mm 15.1*
MFT 4/3" 2 14 mm 334.20 mm 16* 225.57 mm 11.2**
APC-C APS-C 1.5 18.3 mm 239.02 mm 12** 165.12 mm 8.4***
Full-frame format Full-frame format 1 28 mm 155.17 mm 8*** 108.75 mm 5.6

*, **, ***) Here you can see that similar "DOF-relevant" apertures lead to similar DOF ranges; ?) I do not know whether this aperture value can actually be set at the camera, and if so, whether is is created using a neutral density filter.
Note: The results should not be taken as "exact values" because the input data is imprecise to certain degree...

As demonstrated, cameras with small sensors can generally achieve larger "DOF-relevant" apertures and thus larger depth of field ranges than cameras with larger sensors, provided that sufficiently large (physical) aperture values can be set. This corresponds to what you typically experience in practical photography. But of course, there are a few more things to consider, which I would like to discuss in the following.

Diffraction Blur

In cameras with small sensors, diffraction blur occurs at smaller apertures than in those with larger sensors (see Calculating the Optimum Aperture for Different Sensor Sizes (Diffraction Limit)). For this reason, many compact cameras have only a small set of aperture values and generate aperture values partly through the use of gray filters (some compact cameras have only two physical aperture values at all...).

First of all, closing the aperture reduces certain lens errors; on the other hand, increasing diffraction blur cancels out this advantage, so that there is an "optimum aperture" that delivers the best results. My generalized (calculated) results for "optimal apertures" for different sensor types are:

Diffraction blur starts much earlier and is a gradual process. Some authors set the limits for "tolerable diffraction blur" lower than I do, thus, list larger apertures. As the list shows, due to diffraction blur, cameras with small sensors have a smaller aperture range than cameras with large sensors. For cameras with large sensors, lenses with maximum apertures of 22, or even 32 and more can be purchased and thus, also offer a large depth of field. This way, the diffraction blur remains low, but you lose enormously in light intensity. More on this below.

Conclusion: Diffraction blur forces to use a smaller aperture range on cameras with small sensors.

Amount of Light

As clarified in question 2, the amount of light that falls on the sensor at a certain aperture value does not depend on the sensor's size. Cameras with a small sensor therefore have a large depth of field even with large apertures, because the DOF-relevant aperture is applied, so that one can often still take hand-held pictures with it.

Example: Aperture f/8 on a 1" sensor camera corresponds approximately to aperture f/22 on a full-frame camera. That is a difference of three light values (or f-stops)!

Conclusion: Cameras with small sensors need less light because they do not need to be dimmed so far to achieve a large depth of field.

Behavior at High ISO Values

Cameras with a large sensor have a much better (noise) behavior at high ISO values than cameras with a small sensor. Depending on the camera, ISO 800/1600 is the limit for 1" sensors, ISO 1600/3200 for MFT and APS-C cameras, and ISO 6400 or even 12800 are still acceptable for many full-frame cameras, especially for close-up and macro photography.

This allows cameras with a large sensor to, at least in principle, compensate for the problem of light loss when using smaller apertures for greater depth of field. Whether this is actually the case, I cannot decide at the green table; this can only be decided on the basis of the results.

Conclusion: By better behavior at high ISO values, cameras with a large sensor can compensate for the disadvantage of having to be stopped-down further to achieve a large depth of field.

Generally, Large Sensors Offer a Better Image Quality

In general, large sensors are attributed a better image quality than small ones, for example, they offer higher dynamics. If in doubt, this fact might also make the difference to a solution with a small sensor!

Conclusion: Large sensors have further advantages over small sensors, which are reflected in better image quality.

Recap

Whether cameras with large or small sensors have an advantage in close-up and macro photography depends on a number of factors that partially balance each other out, and only in practice will it be possible to decide which solution is better for you. My experience is that close-up and macro photography with compact cameras is much easier. Experiments with cameras with large sensors and macro lenses led to few hits and a lot of frustration, especially in the initial phase...

 

Question 4: Using Depth of Field Markers

When I bought the M-mount expansion unit for my Ricoh GXR and used it with Leica M lenses, I noticed that some parts of the photo were not sharp, although they were located within the depth of field zone for the aperture value that I had used. This "zone" is marked on the lens (see the photos below) and this focusing method is therefore called "zone focusing." Only by chance, I found out that, if one uses a full-frame lens on a camera with smaller sensor, one has to take a different aperture value into account for the depth of field than the one that one has set on the lens. It is important that you do not forget this in the rush of shooting...

Basically, you have to observe the following: If you use full-format lenses on cameras with a smaller sensor, the aperture value must be divided by the crop factor to obtain the aperture value that is relevant for determining the depth of field. For APS-C cameras, the aperture value has to be opened one stop, for MFT cameras it is two stops. This difference is essential to observe when using the depth markings on the lens! For APS-C cameras, the difference between the crop factor of 1.5 and one full f-stop (√2 = 1.414...) is so small that it is sufficient in practice to use the marks of one full f-stop more open.

    

Photos: Distance scale with depth of field marks M-mount lenses - Minolta M-Rokkor 28mm f/2.8 (left) and Voigtländer Color Skopar Pancake II 35mm f/2.5 (right). The left lens is set to an aperture value of f/8, however, the f/5.6 marks have to be considered, because it is mounted to an APS-C camera module!!! For the right lens the non-existing f/2.8 marks would have to be considered if it were mounted to an APS-C camera, because it is set to an aperture value of f/4.

In the literature, I found that the exact aperture value for full-frame format lenses that are used at APS-C cameras is to be changed for about 1.3 and 1.5 f-stops (nevertheless, for simplicity reasons, to open aperture for one f-stop was recommended). Since no details were given there, I had to understand this on my own and looked at the crop factor for various APS-C sensor types in relation to changes in aperture values (if you do not take into account the circle of confusion, but it should be comparable for sensor sizes that similar). The following table illustrates this:

Sensor Type Crop Factor Factor

f-stops
    1.414213562
√2		 1
APS-C (DX) 1.5 (1.51, 1.52) 1.5 < 1 1/3
    1.587401052
√2*6th √2		 1 1/3
APS-C (Canon) 1.6 1.6 < 1 1/2
    1.681792831
√2*4th √2		 1 1/2
Foveon (Sigma) 1.7 1.7 > 1 1/2
MFT 2 2 2

The table shows that the difference is clearly below 1 1/3-stops for "DX" sensors, such as is used in the Ricoh GXR, the Ricoh GR, and the Leica Vario X *. Here, you do not make a significant error when you use the depth markings of the next larger aperture. For APS-C Canon sensors, the difference is about 1 1/3 stops and for Foveon sensors about 1.5 stops - the differences are already more apparent here. For MFT sensors, the reading has already to be changed to two f-stops.

*) The crop factor of 1.5 is pretty much in between a full f-stop of √2 (1.414 ...) and 1 1/3 f-stop increments (1.587).

 

Summary

*) The difference is so small that, in practice, it is sufficient to open one full aperture value, at least when using the DX format.

 

References

 

An den Anfang   Homepage  
gerd (at) waloszek (dot) de

About me
made by walodesign on a mac!
12.06.2018